The Fission Chain Reaction

---

Introduction

---

Nuclear reactors utilize the fission of heavy nuclei, usually an isotope of uranium, namely U-235, to generate heat which is used to make steam to drive turbines and thus to generate electricity.

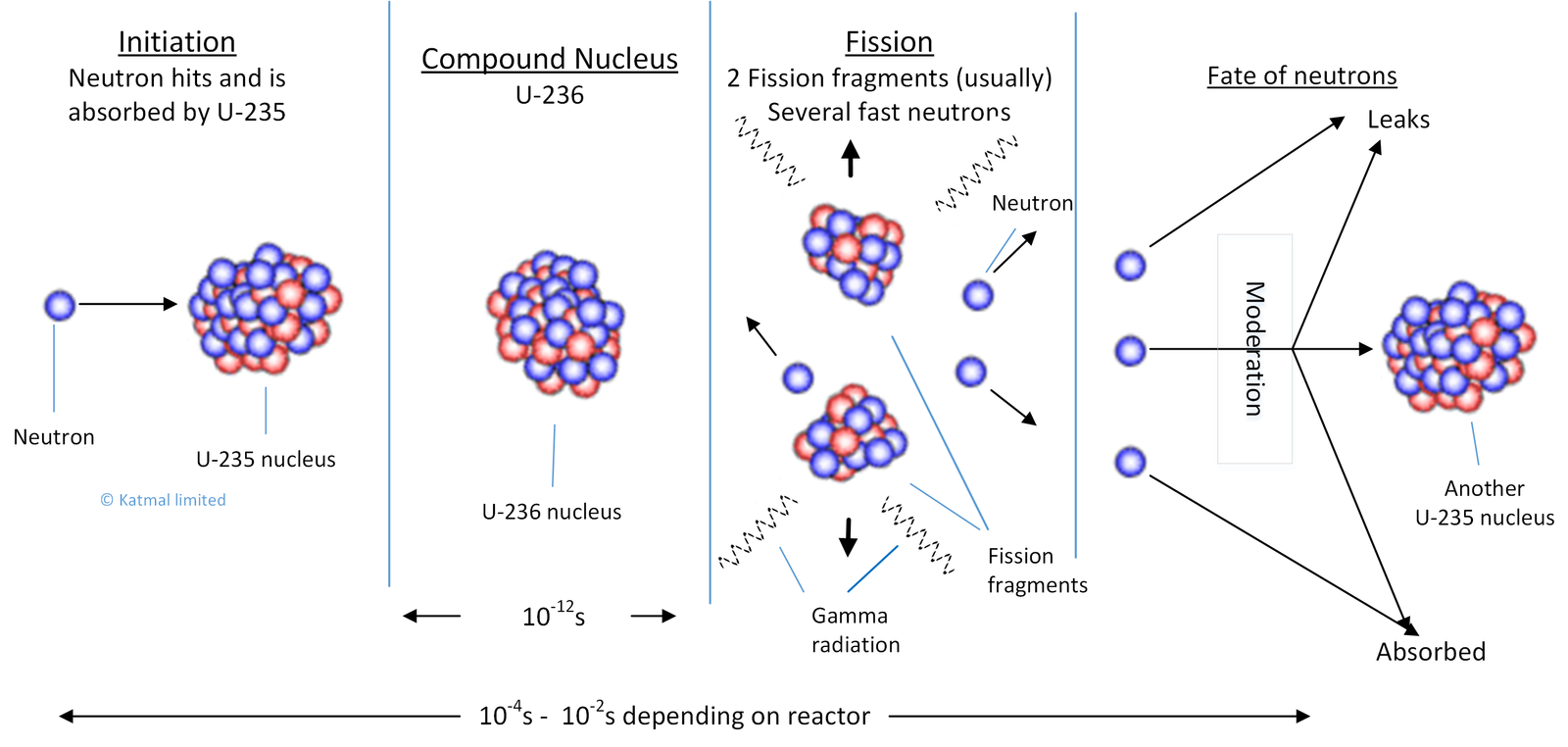
In the chain reaction a thermal (slow moving) neutron is absorbed into the nucleus of a U-235 atom. The U-235 nucleus contains 92 protons and 143 neutrons. Adding another neutron makes the nucleus into unstable excited U-236. Most (about 85.5% ) of the U-236 nuclei undergo a process called “fission”. That is, they split into two (usually ) large fission fragments and a number of fast (highly energetic) neutrons (average about 2.45 for thermal fission of U-235. This takes about 10^-14 seconds and liberates energy.

No of neutrons	0	1	2	3	4	5
Probability (%)	2	17	36	31	12	3

Table Probability distribution of number of neutrons emitted, thermal fission of U-235

The fate of the neutrons

---

Different fates can await the fast neutrons produced in fission; they can fly out of the reactor, they can be absorbed in the reactor internals, they can be slowed down (moderated or thermalized) by interaction with the materials they pass through, and they can go on to induce another fission (more likely after slowing down than before). The equation below is just the mathematical way of presenting these options.

If on average one neutron from each fission goes on to induce another then the rate of reaction will be constant and we say that the reactor is critical. If the average is less than one then the power is reducing and the reactor is sub-critical.

To gain insight into this cycle we introduce the effective multiplication factor k (sometimes shown as k_eff to distinguish it from k_∞ the infinite multiplication factor which applies to infinite sized assembles).

The effective multiplication factor can be expressed as: k = Number of neutrons in a generation /Number of neutron in the previous generation k is a dimensionless number.
k is a measure of the fractional change in the number of neutrons in the reactor over an, as yet unspecified, period of time equivalent to one cycle or “link” of the chain.

It can be shown that:
k = η.f.ρ.ϵ.P_FNL.P_TNL (six-factor equation)

which is an extension of k_∞ = η.f.ρ.ϵ (Fermi’s four-factor formula)

Where:
η = Reproduction factor = (Neutrons produced by fuel)/(Neutrons absorbed by fuel)
f = Thermal utilisation factor = (neutrons absorbed by the fuel)/(neutrons absorbed in total)
ρ = The resonance escape probability = ("Fission neutrons that become thermalised" /"total number of fission neutrons produced" )
ϵ = The fast fission factor = (total number of fission neutrons produced)/(number of fission neutrons from thermal fission)
PFNL = Fast non-leakage probability (The probability that a fast neutron will NOT leak)
PTNL = Thermal non-leakage probability (the probability that a thermal neutron will NOT leak)

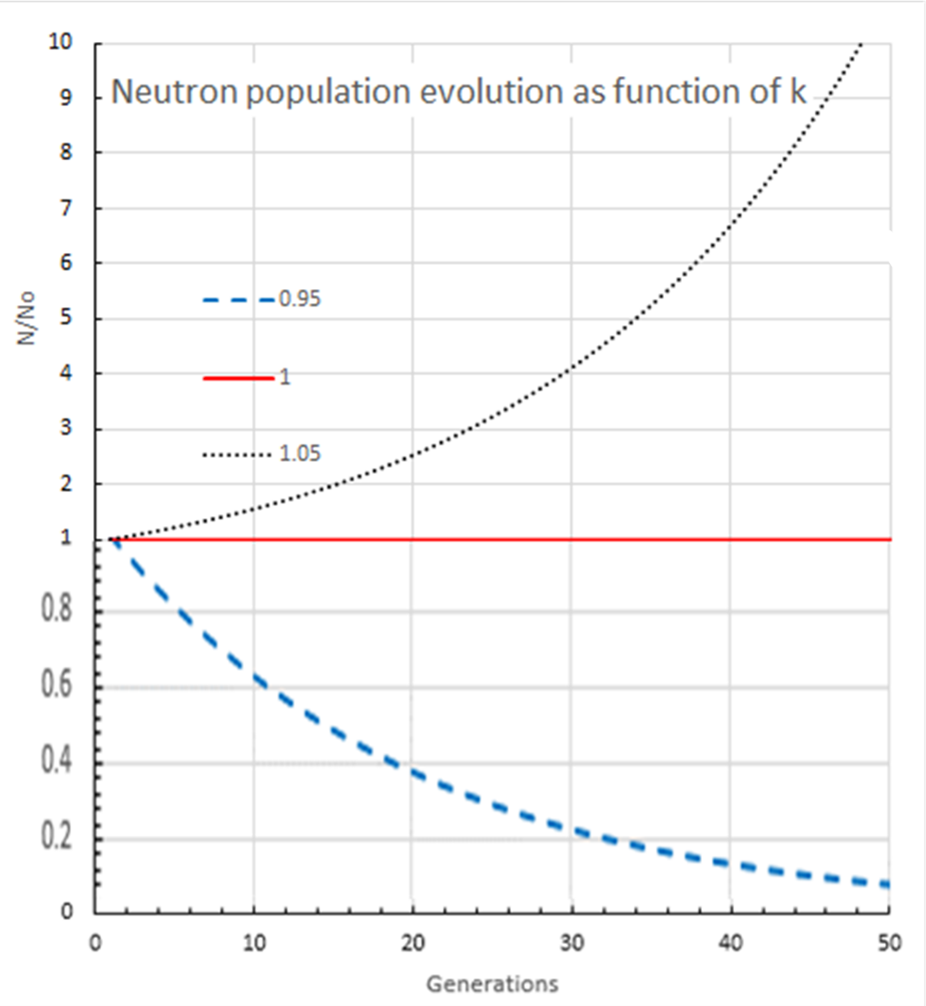
If k is greater than one then the number of neutrons and the power generated by the reactor core is increasing with time. If k is less than one then the reaction is dying away with time (see figure).

The art of running a nuclear reactor is to be able to control k so that power can be raised safety (k > 1 but not too high), kept at constant power (k = 1) and shut down (k <1) when desired.

All of these terms can be affected by the design and operation of the reactor.

Leakage can be reduced by making the reactor bigger, making the material of the reactor better at intercepting neutrons, or by adding an outer layer of material with a low-Z component (that is, contains light nuclei such as hydrogen and carbon) to reflect some of the straying neutrons back into the core (hence the “reflector” you may notice in a number of reactor designs).

Resonance escape can be enhanced by reducing the prevalence of materials that absorb neutrons as they are slowing down, hence the materials used in reactors are carefully chosen and minimum use of materials is made. This term is also sensitive to temperature. This is because a rise in temperature results in greater movement of the atoms in the fuel matrix. This makes it more likely that a neutron will hit a nucleus with an exact energy match between the sum of the kinetic and binding energies of the neutron and the excited state of the resulting nucleus making absorption far more probable as the system does not need to cope with a mismatch of energy. Resonance escape is also enhanced by using heterogeneous reactors. In these the nuclear fuel is in the form of rods or plates surrounded by just the right thickness of moderator. A fast neutron heading out from a fuel pin passes through fuel-less moderator where it loses energy without fear of resonance capture and then enters a fuel rod or plate as a thermalized neutron, below the resonance absorption energies and ready to induce fission. Unenriched U-235 cannot be made to sustain a chain reaction without this trick.

Thermal utilisation can also be enhanced by reducing the amount of neutron absorbing material within the core or by increasing the number of fissile nuclei by enriching the fuel (increasing the proportion of U-235). Further reading Operational factors that affect the multiplication in PWRs

Fission Energy

---

About 85% of the energy produced in fission is the kinetic energy of the fission fragments which is converted to heat within the fuel as they stop within microscopic distances. Some energy is converted to gamma rays emitted at the moment of fission and some is converted to the kinetic energy of the neutrons. Additional energy and neutrons are liberated by the radioactive decay of fission fragments. More detail is given below.

Fission yield

---

There are a large number of possible fission reactions (JEF- 3.3, a database of nuclear reactions, lists 873 isotopes with non-zero independent fission fragment yields for thermal fission of U-235).

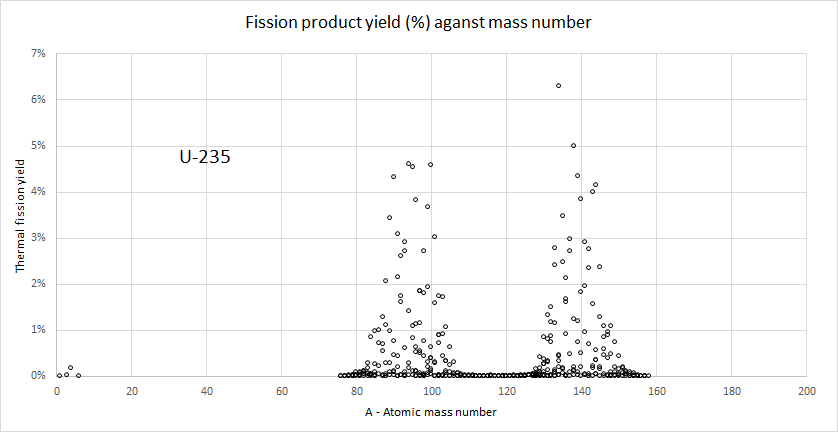
For example

U-235 + n => Ba-144 + Kr-90 + 2n

U-235 + n => Ba-141 + Kr-92 + 3n

U-235 + n => Zr-94 + Te-139 + 3n